COMSOL has the best multiphysical simulation capabilities in my experience. Technical support from Elisa at TECHNIC as well as the engineers at COMSOL has been great.
COMSOL is an important part of our research in plasma physics. We use it in the design of plasma systems and it helps us to obtain a greater understanding of the underlying physics. We have always valued the quick support from TECHNIC and COMSOL and it has been a pleasure to work with them.
Comsol has become a valuable part of our design and decision making process. The exceptional flexibility and access to the physics and solvers in Comsol has allowed us to have deeper understanding on thermomechanical solutions. Technic and Comsol have always been quick and helpful to resolve any issues and provide helpful advice on their products.
At Scion we use COMSOL Multiphysics to understand energy processes, such as the interplay of non-linear solid mechanics and heat & mass transfer during biomass compaction, to design new or more efficient processes.
We use COMSOL Multiphysics to design the customised muffler. With it, we can simulate the insertion loss at different spectrum with different muffler designs.
The Particle Tracing Module extends the functionality of the COMSOL environment for computing the trajectory of particles in a fluid or electromagnetic field, including particle-particle, fluid-particle, and particle-field interactions. You can seamlessly combine any application-specific module with the Particle Tracing Module for computing the fields that drive particle motion. Particles can have mass or be mass-less. The movement is governed by either the Newtonian, Lagrangian, or Hamiltonian formulations from classical mechanics. Boundary conditions can be imposed on the particles on the walls of the geometry to allow particles to freeze, stick, bounce, disappear, or reflect diffusely. User-defined wall conditions may also be specified, where the post collision particle velocity is typically a function of the incoming particle velocity and the wall normal vector. Secondary particles released when an incoming particle strikes a wall can be included. The number of secondary particles and their velocity distribution function can be functions of the primary particle velocity and the wall geometry. Particles can also stick to the wall according to an arbitrary expression or a sticking probability. Additional dependent variables can be added to the model which allows you to compute quantities like particle mass, temperature, or spin.
Particles can be released on boundaries and domains uniformly, according to the underlying mesh, as defined by a grid or according to an arbitrary expression. A wide range of predefined forces is available to describe specifically how the particles interact with the fields. You can then add arbitrary forces as defined by a suitable expression. It is also possible to model the two-way interaction between the particles and the fields (particle-field interaction), as well as the interaction of particles between each other (particle-particle interaction).
Particles are injected from a system of injection nozzles into a CVD chamber with a cone angle of 15 degrees. Initially they have enough inertia to follow their original trajectory but ultimately the drag force takes over and the particles begin to follow the background gas out of the exhaust port.
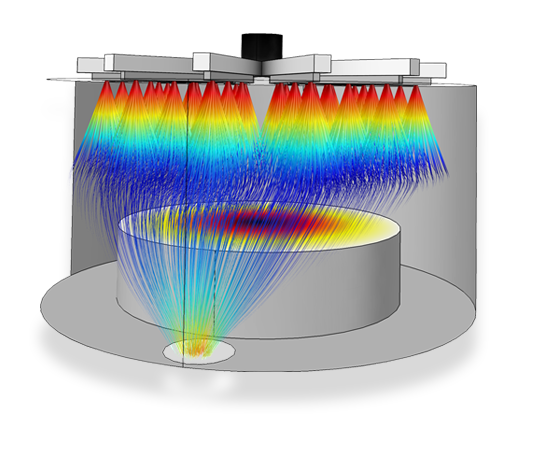
For each particle, an ordinary differential equation is solved for each component of the position vector. This means that three ordinary differential equations are solved for each particle in 3D, and two in 2D. At each time step, the forces acting on each particle are queried from the computed fields at the current particle position. If particle-particle interaction forces are included in the model, they are added to the total force. The particle position is then updated, and the process repeats until the specified end time for the simulation is reached. Since the Particle Tracing Module uses a very general formulation for computing particle trajectories, the Particle Tracing interfaces can be used to model charged particle motion in electromagnetic fields, large scale planetary and galactic movement, and particle motion in laminar, turbulent, and two-phase fluid systems.
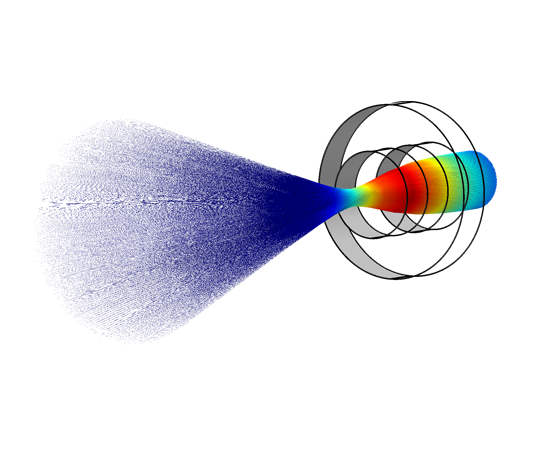
Powerful processing tools allow for sophisticated visualisation of the computed particle trajectories. Particle trajectories can be represented by points, comet tails, arrows, lines, tubes, or ribbons. Animations can easily be created and viewed directly in the graphical user interface (GUI) or exported to file. The particle trajectories can be coloured with arbitrary expressions that can depend on the particles, the fields, or any combination of the two. In cases where the trajectory of many particles are simulated, it is possible to filter out specific particle trajectories according to a logical expression. The group behaviour of the particles can be projected onto a lower dimension and visualised using Poincaré maps or phase portraits. It is also possible to perform operations on the particles to compute and plot the maximum, minimum, average, or integral of some quantity over all the particles. The particle trajectory data itself can be evaluated and written to the Results table or exported to a file. You can conveniently visualise the velocity and energy distributions of the particles, using 1D or 2D histograms.
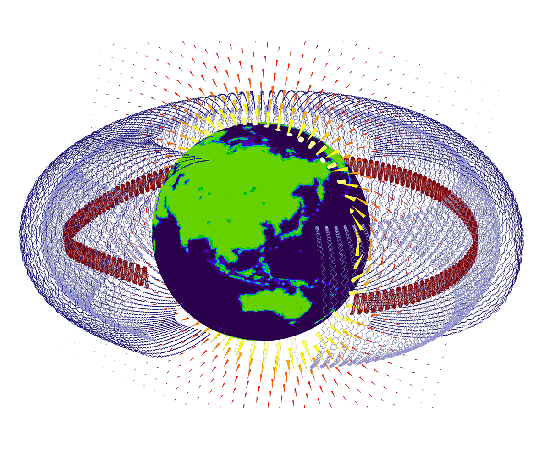
Charged particles, such as electrons, individual ions, or small ion clusters, are affected by three primary forces in electric and magnetic fields:
If the number density of charged species is less than around 1013 1/m3, the effect of the particles on the fields can be neglected. This allows you to compute the fields independently from the particle trajectories. The fields are then used to compute the electric, magnetic, and collisional forces on the particles. The fact that the particle trajectories can be computed in their own study allows efficient and computationally inexpensive iterative solvers to be used.
The motion of microscopic- and macroscopic-sized particles is typically dominated by the drag force acting on particles immersed in a fluid. There are two phases in the system: a discrete phase consisting of bubbles, particles, or droplets, and a continuous phase in which the particles are immersed. In order for the particle tracking approach to be valid, the system should be a dilute or dispersed flow. This means that the volume fraction of the discrete phase should be much smaller than the volume fraction of the continuous phase (generally less than 1%). When the volume fraction of the particles is not small, the fluid system is categorised as a dense flow and you are required to take a different modelling approach. It is important to realise that, with the particle tracking approach, particles do not displace the fluid they occupy.
In a sparse flow, the continuous phase affects the motion of the particles, but not vice versa. This is often referred to as “one-way coupling”. When modelling such a system, it is usually most efficient to solve for the continuous phase first, then to compute the trajectories of the dispersed phases.
In a dilute flow, the continuous phase affects the motion of the particles, and the particle motion in turn disrupts the continuous phase. This is often referred to as “two-way coupling”. In order to model this effect, you must compute the continuous phase and disperse phase simultaneously. Thus, the computational demand is significantly higher when modelling dilute flows than when modelling sparse flows.
In order to fully evaluate whether or not the COMSOL Multiphysics® software will meet your requirements, you need to contact us. By talking to one of our sales representatives, you will get personalised recommendations and fully documented examples to help you get the most out of your evaluation and guide you to choose the best license option to suit your needs.
Fill in your contact details and any specific comments or questions, and submit. You will receive a response from a sales representative within one business day.
Tel: +61 (03) 6224 8690Email: info@technic.com.auConnect on LinkedInGet Your Free TrialCopyright © 2021 Technic Pty Ltd. All Rights Reserved. See our Privacy Policy. Site protected by reCAPTCHA - Privacy | Terms. Website by Gloo.
